投影矩阵
- 关键词:投影矩阵
一、理论基础
一个向量(b)在另一个向量(a)上的投影(实际上就是寻找在a上离b最近的点):
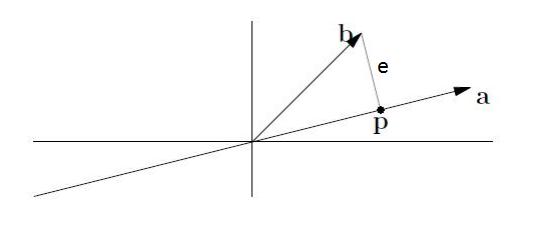
我们假设投影点是向量上的一点p,可以规定 p = xa(x是某个数)。
如果我们把p看作是a的估计值,那么我们定义:e = b - p ,称e为误差。
e与p也就是a垂直,所以有:
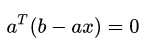
展开化简得到:
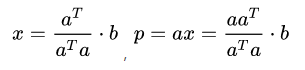
- 如果改变b,那么p相对应改变,然而改变a,p无变化。
二、投影矩阵(projection matrix)
假设一个平面基(basis)是,,那么矩阵 A 的列空间就是该平面。
假设一个不在该平面上的向量 b ,在该平面上的投影是 p 。
任务就是找到合适的 x ,使得 p = Ax 。
e 与该平面垂直,故:
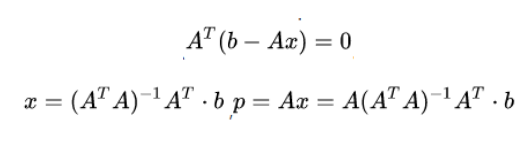
===========================================(进入主题分割线)===================================================
投影矩阵(projection matrix):
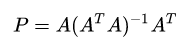
我们最需要关注的是投影矩阵的两个性质:
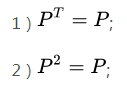
(待更新。。。)
最小二乘法的解与矩阵投影时对变量求解的目标是一致的。
