支持向量机推导及求解过程
- 关键词:支持向量机 – SVM – 推导
一、使用SVM算法的思路
-
它是针对线性可分情况进行分析,对于线性不可分的情况,通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分,从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能;
-
它基于结构风险最小化理论之上在特征空间中建构最优分割超平面,使得学习器得到全局最优化,并且在整个样本空间的期望风险以某个概率满足一定上界。
线性可分情况,把问题转化为一个凸优化问题,可以用拉格朗日乘子法简化,然后用既有的算法解决。
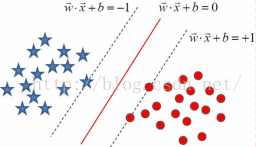
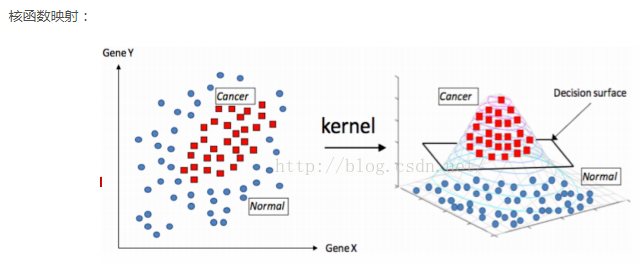
线性不可分情况,用核函数将样本投射到高维空间,使其变成线性可分的情形,利用核函数来减少高纬度计算量。
二、推导过程
输入数据
假设给定一个特征空间上的训练数据集:
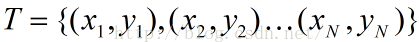
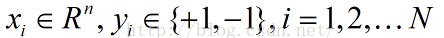
为的类标记,当为+1时,称为正例,当为-1时,称为负例。
线性可分支持向量机
给定线性可分训练数据集,通过间隔最大化得到的分离超平面为:
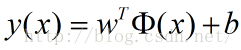
相应的分类决策函数(称为线性可分支持向量机):
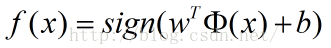
其中包含某个确定的特征空间转换函数,它的作用是将x映射到(更高的)维度,最简单直接的:
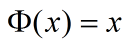
详细推导过程
整理符号

推导目标函数
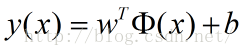
有:
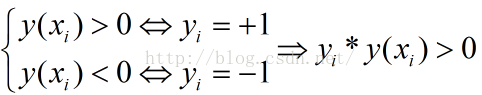
w,b等比例缩放,则t*y的值同样缩放,从而:
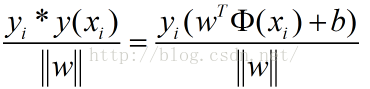
- 最大间隔分离超平面:
目标函数(表示最近点到直线距离尽可能大):
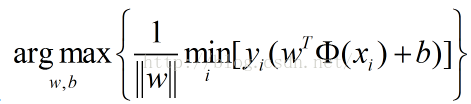
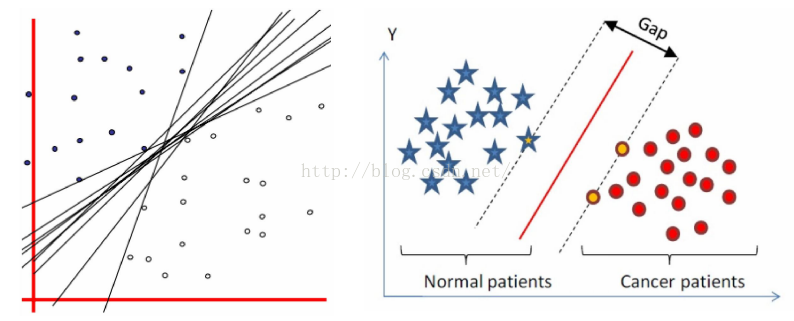
- 函数间隔和几何间隔
函数间隔(分割平面):
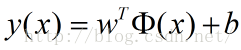
===========================================(我是分割线)===================================================
建立目标函数:




线性不可分支持向量机



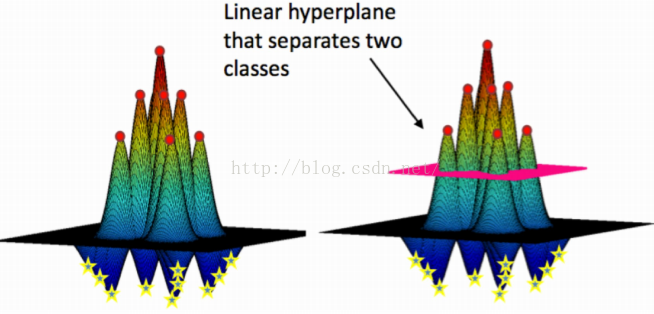
- 核函数:可以使用核函数,将原始输入空间映射到新的特征空间,从而使得原本线性不可分的样本可在核空间可分。
有多项式核函数:

高斯核函数RBF:
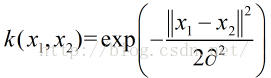
字符串核函数:
在实际应用中,往往依赖先验领域知识或交叉验证等方案才能选择有效的核函数。没有更多先验信息,则使用高斯核函数。
高斯核:
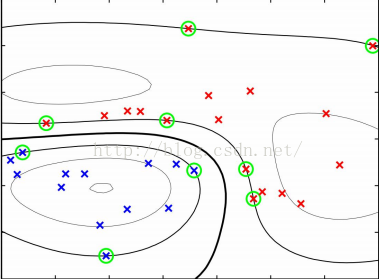
粗线是分割超“平面”,其他线是y(x)的等高线,绿色圈点是支持向量点。高斯核是无穷维的,因为:
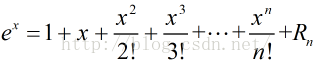
SVM和Logistic回归的比较:
- 经典的SVM,直接输出类别,不给出后验概率;
- Logistic回归,会给出属于哪一个类别的后验概率;
- 比较重点是二者目标函数的异同。
