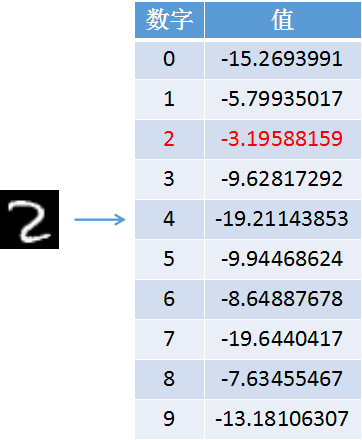
深度置信网络在MNIST数据集中的分类效果

  • 关键词：DBN – MNIST – 特征提取能力探究

一、受限玻尔兹曼机(Restricted Boltzmann Machine)

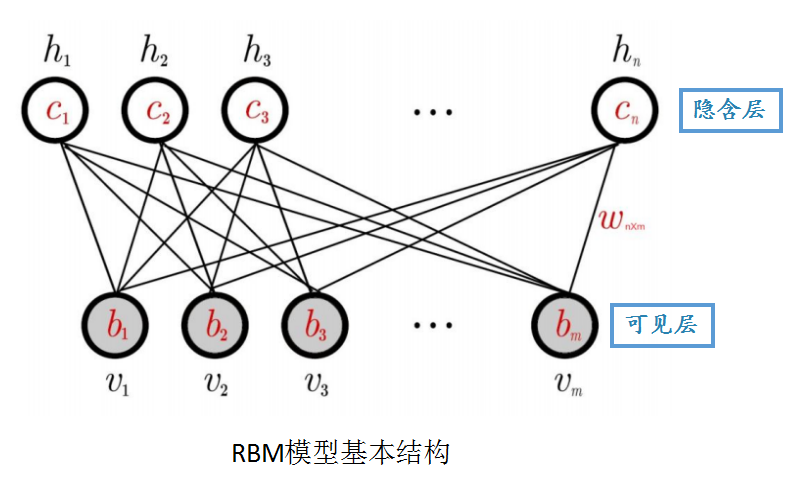
1.RBM网络结构


可见层 隐含层
数据输入 特征提取 权重矩阵 可见层节点的偏移量 隐含层节点的偏移量


image

2.基本原理（引用热平衡理论）

(1) 对于一组给定的状态，当参数确定时，RBM作为一个系统所具备的能量函数定义为：

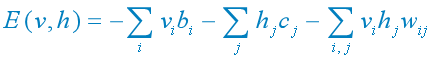
image

(2) 基于该能量函数，可以得到的联合概率分布：

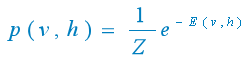
image

其中Z为归一化因子，其定义为：

image

(3) 我们需要关心的是由RBM所定义的关于观测数据v的分布：

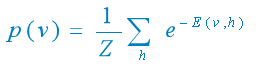
image

(4) 当给定可见单元的状态时，各隐含单元的激活状态之间是条件独立的(σ为sigmoid激活函数)：

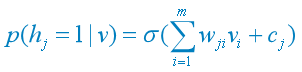
image

(5) 当给定隐含单元的状态时，各可见单元的激活状态之间也是条件独立的：

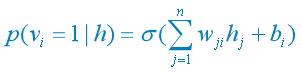
image

3.RBM计算过程

主要目标就是让重构数据越来越接近原始数据：

计算采样（基本一次采样就够）：

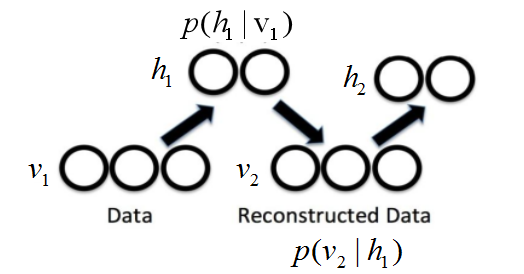
image

重构误差（该值越小越好）：

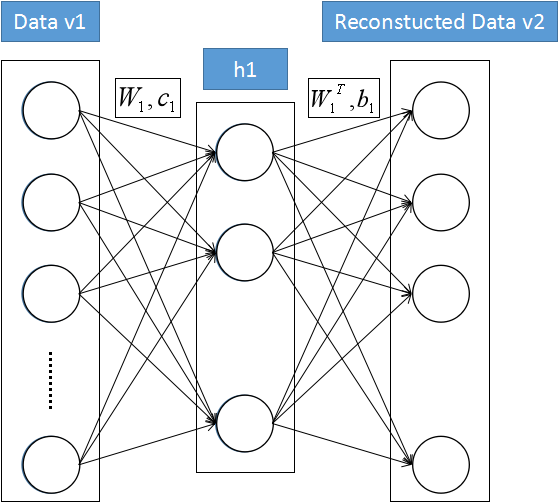
image

过程再现：

image

二、深度置信网络(Deep Belief Network)

1.DBN网络结构

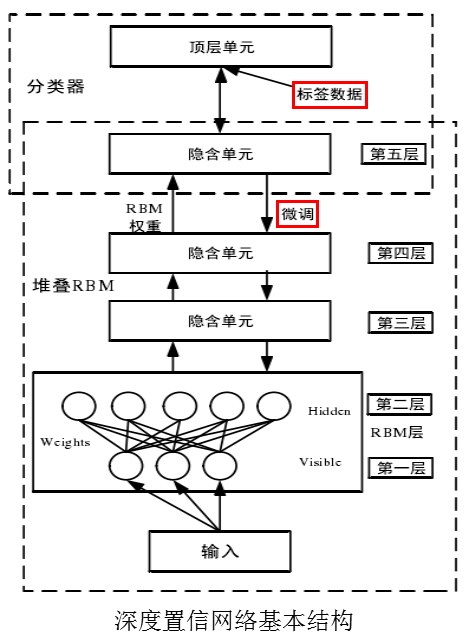
image

2.DBN参数设置

（1）输入层取决于数据维数；

（2）输出层取决于分类类别数；

（3）通过设置一定的网络深度、最大迭代次数和隐含层节点数能够在提取高层次特征同时实现数据降维。

3.DBN如何运用

（1）无监督逐层训练：防止提前收敛、防止陷入局部最优。

（2）有监督微调：提高准确度和精度。

三、深度置信网络在MNIST数据集中的分类效果实践

1.MNIST手写字符数据集

MNIST共有70000条样本，每条样本是由28x28=784个像素点构成的手写字符图像组成，总共有10种字符。

image

用python代码加载MNIST手写字符数据集：

    import numpy as np
    import idx2numpy
    import Image
    import pickle
    import matplotlib.pyplot as plt

    images = idx2numpy.convert_from_file("train-images-idx3-ubyte")
    data=[]
    temp=[]
    for image in images:
        for i in image:
            for j in i:
                temp.append(j)
        data.append(temp)
        temp=[]
    X = np.asarray(data, 'float32')
    # 数据集归一化
    X = X/255.0
    Y = idx2numpy.convert_from_file("train-labels-idx1-ubyte")
    # 测试集10000条
    X_test = X[50000:]
    Y_test = Y[50000:]
    # 训练集50000条
    X = X[:50000]
    Y = Y[:50000]

2.RBM代码结构

调用方式：

sizes = [X.shape[1],输出数据维度]

rbm1 = rbm(sizes)

    class rbm:
        def __init__(self,sizes=[],learning_rate=0.01,numepochs = 1):
            print 'rbm init ,sizes:',sizes,', numepochs:',numepochs
            self.W=np.matrix(np.zeros(sizes,'float32'))
            self.vW=np.matrix(np.zeros(sizes,'float32'))
            self.b=np.matrix(np.zeros(sizes[0],'float32'))
            self.vb=np.matrix(np.zeros(sizes[0],'float32'))
            self.c=np.matrix(np.zeros(sizes[1],'float32'))
            self.vc=np.matrix(np.zeros(sizes[1],'float32'))
            self.learning_rate = learning_rate
            self.numepochs = numepochs
            self.v1=self.b
            self.v2=self.b
            self.h1=self.c
            self.h2=self.c
            self.c1=self.W
            self.c2=self.W
        def sigmrnd(self,X):
            return np.float32(1./(1.+np.exp(-X)) > np.random.random(X.shape))
        def train(self,X):
            print 'begin train , X.shape',X.shape,'numepochs:',self.numepochs
            for i in range(self.numepochs):
                err = 0
                for v in X:
                    self.v1 = np.matrix(v)
                    self.h1 = self.sigmrnd(self.c+np.dot(self.v1,self.W))
                    self.v2 = self.sigmrnd(self.b+np.dot(self.h1,self.W.T))
                    self.h2 = self.sigmrnd(self.c+np.dot(self.v2,self.W))
                    self.c1 = np.dot(self.h1.T,self.v1).T
                    self.c2 = np.dot(self.h2.T,self.v2).T
                    self.vW = self.learning_rate*(self.c1-self.c2)
                    self.vb = self.learning_rate*(self.v1-self.v2)
                    self.vc = self.learning_rate*(self.h1-self.h2)
                    self.W = self.W + self.vW
                    self.b = self.b + self.vb
                    self.c = self.c + self.vc
                    err = err + np.linalg.norm(self.v1-self.v2)
                print "err :", err
            return self.W,self.b,self.c
        def predict(self,X):
            m,n = X.shape
            return self.sigmrnd(np.dot(np.ones((m,1)),self.c)+np.dot(X,self.W))

3.DBN代码结构

调用方式：

dbn1 = dbn(sizes,学习率,采样迭代次数)

    class dbn:
        def __init__(self,sizes = [],learning_rate = 0.01,numepochs = 1):
            print 'dbn init ,sizes:',sizes,', numepochs:',numepochs
            self.sizes = sizes
            self.rbms = []
            self.learning_rate = learning_rate
            self.numepochs = numepochs
            self.X = []
            for i in range(len(self.sizes)-1):
                self.rbms.append(rbm(sizes[i:i+2],0.01,self.numepochs))
        def train(self,X):
            self.X.append(X)
            for j in range(len(self.sizes)-1):
                self.rbms[j].train(self.X[j])
                self.X.append(self.rbms[j].predict(self.X[j]))
        def predict(self,X):
            for j in range(len(self.sizes)-1):
                X = self.rbms[j].predict(X)
            return X

4.其他函数

Softmax分类器

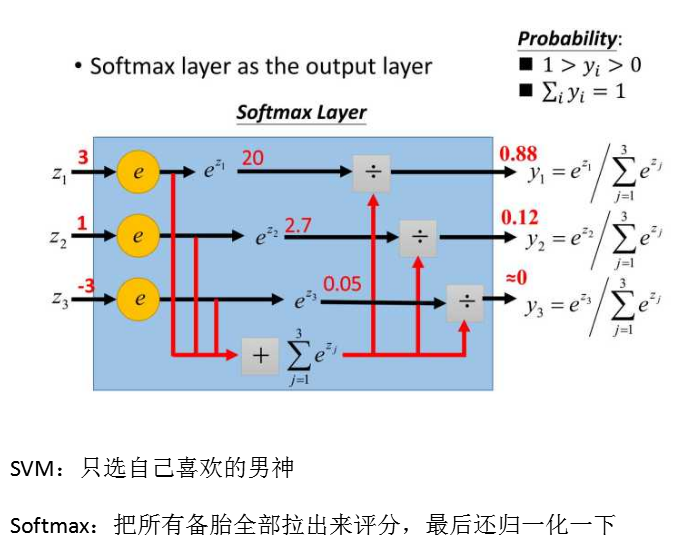
image

    # 激活函数
    def sigmoid(X):
         return 1.0/(1.0+np.exp(-X))
    # 随机梯度下降
    def gradAscent(data,labels,label):
        m,n=data.shape
        alpha = 0.01
        weights = np.ones((n,1))
        print 'gradAscent begin'
        numiter = 1
        for j in range(numiter):
            dataIndex=range(m)
            for i in range(m):
                alpha = 4.0/(1.0+j+i)+0.01
                randIndex = int(np.random.uniform(0,len(dataIndex)))
                h = sigmoid(sum(data[randIndex]*weights))
                err = float(labels[randIndex]==label) - h
                weights = weights + alpha * (data[randIndex].T) * err
                del(dataIndex[randIndex])
        return weights

5.网络整体结构

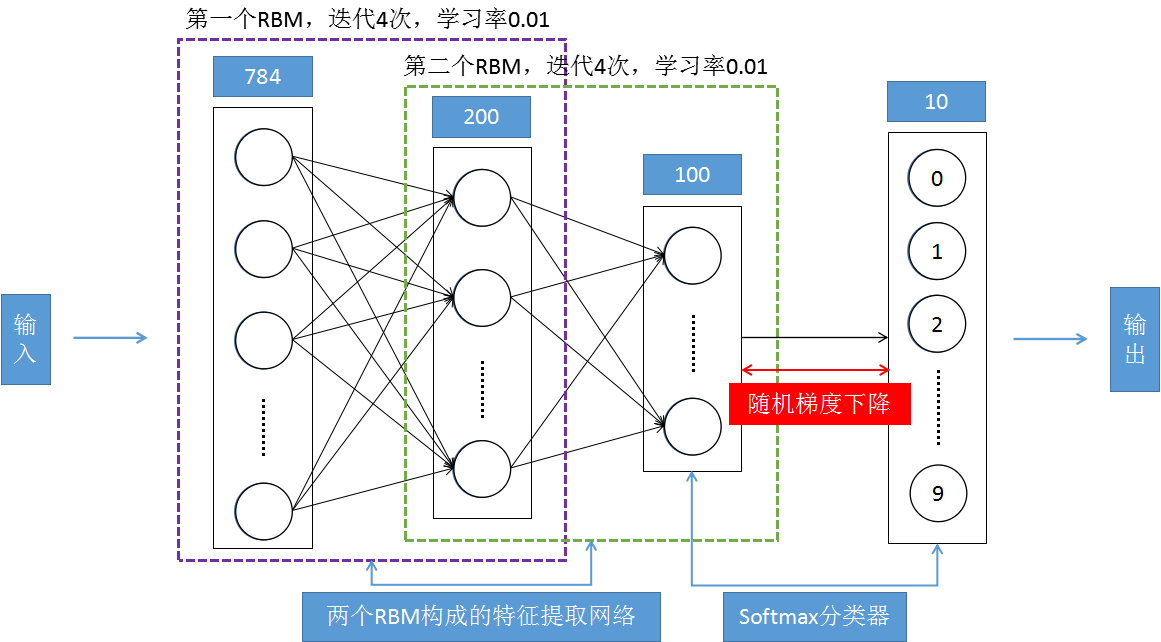
image

6.实践结果

(1)结果一：整体结果，每一个分子是预测准确的数据个数，分母是对应该类数字的全部个数

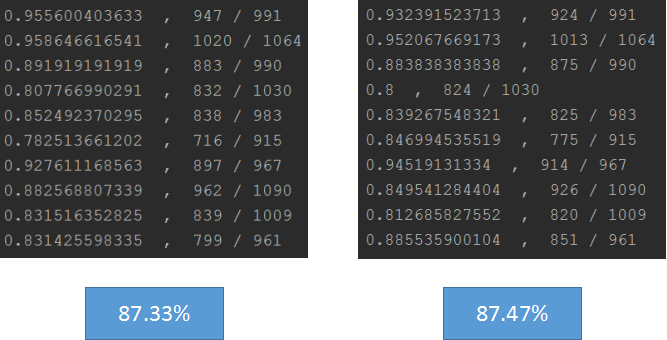
image

(2)结果二：输入图片，得到结果如下

image